- Index
- Bienvenue sur le site WEB "industry-finder".
- Résolution du Conseil, du 7 mai 1985, concernant une nouvelle approche
- Nouveau guide bleu pour la mise en oeuvre des directives européennes pour les produits règles 2016
- l'éco-conception et les produits industriels
- le marquage CE des machines
- Le nouveau guide bleu daté de avril 2014
- Directive Machines
- Historique de la directive machines 2006/42/CE
- Directive machines 2006/42/CE
- Considerants de la directive machines 2006/42/CE
- Articles de la directive machines 2006/42/CE
- Article 1 de la directive machine 2006/42/CE - Champ d'application
- Article 2 de la directive machine 2006/42/CE - Definitions
- Article 3 de la directive machine 2006/42/CE - Directives particulières
- Article 4 de la directive machine 2006/42/CE - Surveillance du marché
- Article 5 de la directive machine 2006/42/CE - Mise sur le marché et mise en service
- Article 6 de la directive machine 2006/42/CE - Libre circulation
- Article 7 de la directive machine 2006/42/CE - Présomption de conformité et normes harmonisées
- Article 8 de la directive machine 2006/42/CE - Mesures spécifiques
- Article 9 de la directive machine 2006/42/CE - Mesures particulières visant des machines potentiellement dangereuses
- Article 10 de la directive machine 2006/42/CE - Procédure de contestation d'une norme harmonisée
- Article 11 de la directive machine 2006/42/CE - Clause de sauvegarde
- Article 12 : Procédures d'évaluation de la conformité des machines - directive machines 2006/42/CE
- Article 13 de la directive machine 2006/42/CE - Procédure pour les quasi-machines
- Article 14 de la directive machine 2006/42/CE - Organismes notifiés
- Article 15 de la directive machine 2006/42/CE - Installation et utilisation des machines
- Article 16 de la directive machine 2006/42/CE - Marquage CE
- Article 17 de la directive machine 2006/42/CE - Marquage non conforme
- Article 18 de la directive machine 2006/42/CE - Confidentialité
- Article 19 de la directive machine 2006/42/CE - Coopération entre les États membres
- Article 20 de la directive machine 2006/42/CE - Voies de recours
- Article 21 de la directive machine 2006/42/CE - Diffusion de l'information
- Article 22 de la directive machine 2006/42/CE - Comité
- Article 23 de la directive machine 2006/42/CE - Sanctions
- Article 24 de la directive machine 2006/42/CE - Modification de la directive 95/16/CE
- Article 25 : Abrogation de la directive machines 2006/42/CE
- Article 26 : Transposition - directive machines 2006/42/CE
- Article 27 : Dérogation - directive machines 2006/42/CE
- Article 28 : Entrée en vigueur - directive machine 2006/42/CE
- Article 29 : Destinataires - directive machine 2006/42/CE
- ANNEXE I de la directive machines - sommaire
- principes généraux - annexe 1 directive machines 2006/42/CE
- 1 EXIGENCES ESSENTIELLES DE SANTE ET DE SECURITE - definitions - Annexe I de la directive machines 2006/42/CE
- Article 1.1.2. Principes d'intégration de la sécurité - Annexe I de la directive machines 2006/42/CE
- Article 1.1.3. Matériaux et produits - Annexe I de la directive machines 2006/42/CE
- Article 1.1.4. Éclairage - Annexe I de la directive machines 2006/42/CE
- Article 1.1.5. Conception de la machine en vue de sa manutention - Annexe I de la directive machines 2006/42/CE
- Article 1.1.6. Ergonomie - Annexe I de la directive machines 2006/42/CE
- Article 1.1.7. Poste de travail - Annexe I de la directive machines 2006/42/CE
- Article 1.1.8. Siège - Annexe I de la directive machines 2006/42/CE
- Article 1.2.1. Sécurité et fiabilité des systèmes de commande - annexe 1 de la directive machines 2006/42/CE
- Article 1.2.2. Organes de service - Annexe I de la directive machines 2006/42/CE
- Article 1.2.2. Organes de service - Annexe I de la directive machines 2006/42/CE
- Article 1.2.3. Mise en marche - Annexe I de la directive machines 2006/42/CE
- Articles 1.2.4. Arrêt, arrêt normal, arrêt d'urgence - Annexe I de la directive machines 2006/42/CE
- Article 1.2.4.4. Ensembles de machines - Annexe I de la directive machines 2006/42/CE
- Article 1.2.5. Sélection des modes de commande ou de fonctionnement - Annexe I de la directive machines 2006/42/CE
- Article 1.2.6. Défaillance de l'alimentation en énergie - Annexe I de la directive machines 2006/42/CE
- Article 1.3. MESURES DE PROTECTION CONTRE LES RISQUES MÉCANIQUES - Annexe I de la directive machines 2006/42/CE
- Article 1.4. CARACTÉRISTIQUES - PROTECTEURS ET DISPOSITIFS DE PROTECTION - Annexe I de la directive machines 2006/42/CE
- Article 1.5. RISQUES DUS À D'AUTRES DANGERS - Annexe I de la directive machines 2006/42/CE
- Article 1.6. ENTRETIEN - Annexe I de la directive machines 2006/42/CE
- Article 1.7. INFORMATION - Annexe I de la directive machines 2006/42/CE
- Article 2. EXIGENCES COMPLÉMENTAIRES POUR CERTAINES CATÉGORIES DE MACHINES - Annexe I de la directive machines 2006/42/CE
- Article 3. EXIGENCES POUR PALLIER LES DANGERS DUS À LA MOBILITÉ DES MACHINES - Annexe I de la directive machines 2006/42/CE
- Article 4. EXIGENCES COMPLÉMENTAIRES - DANGERS DUS AUX OPÉRATIONS DE LEVAGE - Annexe I directive machines 2006/42/CE
- Article 5. EXIGENCES COMPLÉMENTAIRES MACHINES DESTINÉES À DES TRAVAUX SOUTERRAINS - Annexe I de la directive machines 2006/42/CE
- Article 6. EXIGENCES COMPLÉMENTAIRES DANGERS DUS AU LEVAGE DE PERSONNES - Annexe I de la directive machines 2006/42/CE
- Annexe II de la directive machines 2006/42/CE - déclaration CE de conformité
- Annexe III de la directive machines 2006/42/CE - marquage CE
- Annexe IV de la directive machines 2006/42/CE
- Annexe V de la directive machines 2006/42/CE - Liste des composants de sécurité
- Annexe VI de la directive machines 2006/42/CE - Notice d'assemblage d'une quasi-machine
- Annexe VII de la directive machines 2006/42/CE - Dossier technique pour les machines et les quasi-machines
- Annexe VIII directive machines 2006/42/CE - Évaluation de la conformité avec contrôle interne de fabrication d'une machine
- Annexe IX de la directive machines 2006/42/CE - Examen CE de type
- Annexe X de la directive machines 2006/42/CE - Assurance qualité complète
- Annexe XI directive machines 2006/42/CE - Critères minimaux pour la notification des organismes notifiés
- Annexe XII directive machines 2006/42/CE - Tableau de correspondance entre directive machines 2006/42/CE et directive 1998/37/CE
- Directive machines 98/37/CE
- considérants de la directive machines 1998/37/CE
- articles de la directive machines 1998/37/CE
- Annexe I de la directive machines 1998/37/CE
- Annexe II de la directive machines 1998/37/CE
- Annexe III de la directive machines 1998/37/CE
- Annexe IV de la directive machines 1998/37/CE
- Annexe V de la directive machines 1998/37/CE
- Annexe VI de la directive machines 1998/37/CE
- Annexe VII de la directive machines 1998/37/CE
- Annexe VIII de la directive machines 1998/37/CE
- Annexe IX de la directive machines 1998/37/CE
- Directive machines 1989/392/CE
- Considérants de la directive machines 1989/392/CEE
- articles de la directive machines 1989/392/CEE
- Annexe I de la directive machines 1989/392/CEE
- Annexe II de la directive machines 1989/392/CEE
- Annexe III de la directive machines 1989/392/CEE
- Annexe IV de la directive machines 1989/392/CEE
- Annexe V de la directive machines 1989/392/CEE
- Annexe VI de la directive machines 1989/392/CEE
- Annexe VII de la directive machines 1989/392/CEE
- Amendements de la directive machines 1989/392/CEE
- guide de la Direction Générale du Travail modifications de machines
- Directives ATEX
- Directive ATEX 94/9/CE
- Considerants de la directive ATEX 94/9/CE
- Articles de la directive ATEX 94/9/CE
- Article 1 de la directive ATEX 94/9/CE
- Article 2 de la directive ATEX 94/9/CE
- Article 3 de la directive ATEX 94/9/CE
- Article 4 de la directive ATEX 94/9/CE
- Article 5 de la directive ATEX 94/9/CE
- Article 6 de la directive ATEX 94/9/CE
- Article 7 de la directive ATEX 94/9/CE
- Article 8 de la directive ATEX 94/9/CE
- Article 9 de la directive ATEX 94/9/CE
- Article 10 de la directive ATEX 94/9/CE
- Article 11 de la directive ATEX 94/9/CE
- Article 12 de la directive ATEX 94/9/CE
- Article 13 de la directive ATEX 94/9/CE
- Article 14 de la directive ATEX 94/9/CE
- Article 15 de la directive ATEX 94/9/CE
- Article 16 de la directive ATEX 94/9/CE
- ANNEXE I de la directive ATEX 94/9/CE : CRITÈRES DÉTERMINANT LA CLASSIFICATION DES GROUPES D'APPAREILS EN CATeGORIES
- ANNEXE II de la directive ATEX 94/9/CE : EXIGENCES ESSENTIELLES DE SeCURITe ET de SANTE
- ANNEXE III de la directive ATEX 94/9/CE : MODULE: EXAMEN CE DE TYPE
- ANNEXE IV de la directive ATEX 94/9/CE : MODULE: ASSURANCE QUALITE DE PRODUCTION
- ANNEXE V de la directive ATEX 94/9/CE : MODULE VÉRIFICATION SUR PRODUIT
- ANNEXE VI de la directive ATEX 94/9/CE : MODULE CONFORMITE AU TYPE
- ANNEXE VII de la directive ATEX 94/9/CE : MODULE ASSURANCE QUALITE DU PRODUIT
- ANNEXE VIII de la directive ATEX 94/9/CE : MODULE CONTROLE INTERNE DE FABRICATION
- ANNEXE IX de la directive ATEX 94/9/CE : MODULE: VERIFICATION À L'UNITE
- ANNEXE X de la directive ATEX 94/9/CE : marquage CE et contenu de la declaration CE de conformite
- ANNEXE XI de la directive ATEX 94/9/CE: NOTIFICATION DES ORGANISMES
- Directive ATEX 99/92/CE
- Directive ATEX 2014/34/UE
- Considérants de la directive ATEX 2014/34/UE
- les articles de la directive ATEX 2014/34/UE
- Annexe 1 de la directive ATEX 2014/34/UE
- Annexe 2 de la directive ATEX 2014/34/UE
- Annexe 3 de la directive ATEX 2014/34/UE
- Annexe 4 de la directive ATEX 2014/34/UE
- Annexe 5 de la directive ATEX 2014/34/UE
- Annexe 6 de la directive ATEX 2014/34/UE
- Annexe 7 de la directive ATEX 94/9/EC
- Annexe 8 de la directive ATEX 2014/34/UE
- Annexe 9 de la directive ATEX 2014/34/UE
- Annexe 10 de la directive ATEX 2014/34/UE
- Annexe 11 de la directive ATEX 2014/34/UE
- Annexe 12 de la directive ATEX 2014/34/UE
- La nouvelle directive ATEX
- Audits dans le domaine Ex - EN 13980, OD 005 et EN ISO / CEI 80079-34
- La déclaration CE de conformité en ATEX
- Directive ATEX 94/9/CE
- IECEX
- Normalisation & réglementation européenne
- Sécurité des machines - réglementation européenne et normalisation
- Réglementation européenne sur les machines - normes harmonisées
- Sécurité des machines : normalisation et réglementation européenn
- Normalisation dans le secteur des machines
- FD ISO/TR 14121-2 - Février 2008
- ISO 11161:2007
- ISO 13849-1:2006
- ISO 13849-2:2012
- ISO 13850:2006 - Sécurité des machines -- Arrêt d'urgence -- Principes de conception
- ISO 13851:2002 - Sécurité des machines -- Dispositifs de commande bimanuelle -- Aspects fonctionnels et principes de conception
- ISO 13854:1996 - Sécurité des machines -- Écartements minimaux pour prévenir les risques d'écrasement de parties du corps humain
- ISO 13854:1996 Sécurité des machines -- Écartements minimaux pour prévenir les risques d'écrasement de parties du corps humain
- ISO 13855:2010 - Safety of machinery -- Positioning of safeguards with respect to the approach speeds of parts of the human body
- ISO 13856-1:2013 Sécurité des machines -- Dispositifs de protection sensibles à la pression -- Partie 1
- ISO 13856-2:2013 - Sécurité des machines -- Dispositifs de protection sensibles à la pression -- Partie 2: Principes généraux
- ISO 13856-3:2013 Sécurité des machines -- Dispositifs de protection sensibles à la pression - Partie 3
- ISO 13857:2008 Sécurité des machines - Distances de sécurité - zones dangereuses
- ISO 14119:2013- Dispositifs de verrouillage associés à des protecteurs
- ISO 14120:2002 -Protecteurs - Prescriptions generales pour la conception et la construction
- ISO 14122-2:2001 - Moyens d'acces permanents aux machines
- ISO 14122-3:2001- Moyens d'acces permanents aux machines
- ISO 14122-4:2004 - Moyens d'acces permanents aux machines
- ISO 14123-1:1998 - Reduction des risques pour la sante resultant de substances dangereuses emises par des machines
- ISO 14123-2:1998 - Reduction des risques pour la sante resultant de substances dangereuses emises par des machines -- Partie 2
- ISO 14159:2002 - Prescriptions relatives à l'hygiene lors de la conception des machines
- ISO 19353:2005 Securite des machines - Prevention et protection contre l'incendie
- ISO/DTR 22100-2 - Securite des machines - Partie 2: La relation entre l'ISO 12100 et l'ISO 13849
- ISO/TR 14121-2:2012 - Appréciation du risque - Partie 2: Lignes directrices pratiques et exemples
- ISO/TR 18569:2004 - Lignes directrices pour la comprehension et l'utilisation des normes sur la securite des machines
- ISO/TR 23849:2010 - Lignes directrices relatives à l'application de l'ISO 13849-1 et de la CEI 62061
- NF EN ISO 12100 Novembre 2010
- NF EN ISO 12100-1 - Janvier 2004
- NF EN ISO 12100-1/A1 Août 2009
- NF EN ISO 12100-2 JANVIER 2004
- NF EN ISO 12100-2/A1 Août 2009
- NF EN ISO 14121-1 - Novembre 2007
- Liste des normes harmonisées - directive machines 2006/42/CE
- Liste des normes harminisées - directive machines 2006/42/CE - 09.06.2017
- Liste des normes harmonisées - directive machines - OJ C 2016/C173/01 du 15/05/2016
- Liste des normes harmonisées - directive machines 2006/42/CE - corrigendum OJ C 2015/C 087/03 du 13/03/2015
- Liste des normes harmonisées - directive machines - OJ C 2015/C 054/01 du 13/02/2015
- Liste des normes harmonisées - directive machines - OJ C 220 du 11/07/2014
- Liste des normes harmonisées - directive machines - OJ C 110 du 11/04/2014
- Liste des normes harmonisées - directive machines - OJ C 348 du 28/11/2013
- Liste des normes harmonisées directive machines - OJ C 099 du 05/04/2013
- Guide d'application de la directive machines 2006/42/CE, recommendations for use - normes harmonisées
- recommendation for use - directive machines 2006/42/CE
- Organismes notifiés au titre de la directive machines 2006/42/CE
- Sécurité de matériels et équipements EX, IECEx : Normalisation - réglementation européenne
- Normalisation dans le domaine des ATEX et des Ex
- liste des normes harmonisées - directive ATEX 94/9/CE
- Liste des normes harmonisées directive ATEX 2014/34/UE - 12-10-2018
- Harmonized standards list ATEX 94/9/EC directive - OJ C 126 - 08/04/2016
- Liste des normes harmonisées directive ATEX 94/9/CE - OJ C 335 - 09/10/2015
- Liste des normes harmonisées directive ATEX 94/9/CE - OJ-C 445-02 - 12/12/2014
- Liste des normes harmonisées directive ATEX 94/9/CE - OJ-C 076-14/03/2014
- Liste des normes harmonisées - directive ATEX 94/9/CE - OJ-C 319 05/11/2013
- Réglementation européenne pour la directive ATEX 94/9/CE
- Guide d'application de la directive ATEX 94/9/CE
- Guide d'application de la directive ATEX 2014/34/UE
- Alignement de dix directives d’harmonisation technique sur la décision n° 768/2008/CE
- Sécurité des machines - réglementation européenne et normalisation
- Dernières news
- Sécurité fonctionnelle
- Les dispositifs de sécurité en ATEX
- Historique des normes de sécurité fonctionnelle et directive machines
- Sécurité fonctionnelle
- Principes de sécurité éprouvés : l'action mécanique positive
- la sécurité fonctionnelle et les réseaux de terrain
- les microprocesseurs dans les techniques de sécurité
- principes de conception sûr - Les relais de sécurité et les machines
- prévention de la mise en marche intempestive norme EN 1037+A1
- Sécurité fonctionnelle - les codes détecteurs d'erreur - parité et chechsum
- Sécurité fonctionnelle - les codes détecteurs d'erreur - le CRC et les codes de Hamming
- Nouveau règlement machines 2023/1230
Sécurité fonctionnelle - les codes détecteurs d'erreur - le CRC et les codes de Hamming
Soit un mot "m" de "n" digits :
m = (a1, a2, a3, a4, a5, a6, a7, a8) avec ai= 0 ou 1
en associant un polynome on obtient :
m(x) = a1x7 + a2x6 + a3x5 + a4x4 + a5x3 + a6x2 + a7x + a8
Lemme :
- si un mot m de n digits peut représenter un message (il fait partie du code) alors toute permutation circulaire fait également partie du code.
- en algèbre modulo 2, l'addition et la soustraction sont identiques
Chaque mot transmis "C" comporte :
C(x) = m(x) + K(x)
C(x) = g(x) X Q(x)
avec g(x) = polynome générateur
d'ou :
m(x) = g(x) X Q(x) + K(x) - (+ K(x) car en algèbre modulo 2, l'addition et la soustraction sont identiques)
avec K(x) = reste de la division de m(x) par g(x)
Exemple :
C(x) = m(x) + K(x)
[1 1 0 1 a5 a6 a7] = [1 1 0 1 0 0 0 ]  [a5 a6 a7]
[a5 a6 a7]
soit m = [1 1 0 1]
en posant g(x) = x3 + x + 1
en associant un polynome g(x) = x3 + x + 1 à m on obtient m(x) - Cf. ci-avant :
m(x) = x6 +x5 + x3
En divisant m(x) / g(x), on obtient : x6 + x5 + .. + x3 | x3 + x + 1
| x6 + x5 + .. + x3 | x3 + x + 1 |
 [x6 + .. + x4 + x3] [x6 + .. + x4 + x3] |
(x3 + x2) + x + 1 |
| = x5 + x4 | |
 [x5 + .. + x3 + x2] [x5 + .. + x3 + x2] |
|
| = x4 + x3 + x2 | |
 [x4 + .. + x2 + x] [x4 + .. + x2 + x] |
|
| = x3 + .. + x | |
 [x3 + .. + x + 1] [x3 + .. + x + 1] |
|
| (reste) 1 |
Le reste : 1 = 0 x2 + 0 x + 1
Le reste peut s'écrire 1 = [0 0 1] qui est le groupe de contrôle
Le mot final transmis est [1 1 0 1 0 0 1]
Application à la génération d'un CRC
le message à diviser est présenté bits de poids forts en tête, soit
poids faible [0 0 0 1 0 1 1] poids fort
| Registres | Reste des divisions par g(x) |
|||||
| Etat | Bit transmis | 1 | 2 | 3 | ||
| INIT | / | 0 | 0 | 0 | ||
| 1er coup | 1 | 1 | 0 | 0 | ||
| 2eme coup | 1 | 1 | 1 | 0 | ||
| 3eme coup | 0 | 0 | 1 | 1 | ||
| 4eme coup | 1 | 0 | 1 | 1 | 0x3 + x4 + x5 | Reste de la division / x3 |
| 5eme coup | 0 | 1 | 1 | 1 | x2 + x3 + x4 | Reste de la division / x2 |
| 6eme coup | 0 | 1 | 0 | 1 | x + 0x2 + x3 | Reste de la division / x |
| 7eme coup | 0 | 1 | 0 | 0 | 1 + 0x + 0x2 | Reste de la division /1 |
Les coefficients du polynome diviseur sont matérialisés par des interrupteurs
Les informations sont stockées dans des registres
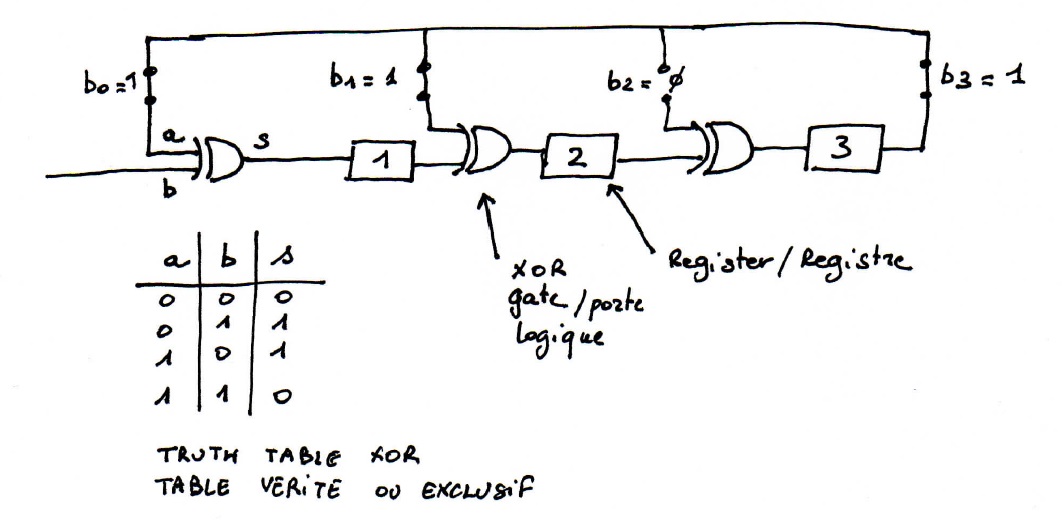
- A l'init, les registres sont vides
- A l'issue des "k" impulsions nous avons dans les registres les valeurs an-k-1, ..., an-1, an
A l'impulsion suivante, nous avons le registre qui a pour valeur la nouvelle entrée  la sortie. Les valeurs des registres sont donc :
la sortie. Les valeurs des registres sont donc :
- Valeur du registre 1 = an-k-2
 anbo (dans notre cas = an-k-2
anbo (dans notre cas = an-k-2  an car (bo=1)
an car (bo=1) - Valeur du registre 2 = an-k-1
 anb1
anb1 - Valeur du registre 3 = an-k
 anb2
anb2
On constate en effectuant la division m(x) / g(x)
- que le premier reste est le contenu des registres 1, 2, 3, ... k
- au (n - k + 1)ème coup, le reste cherché se trouve dans le registre
1. Le C.R.C. (Cyclic Redundancy Check)
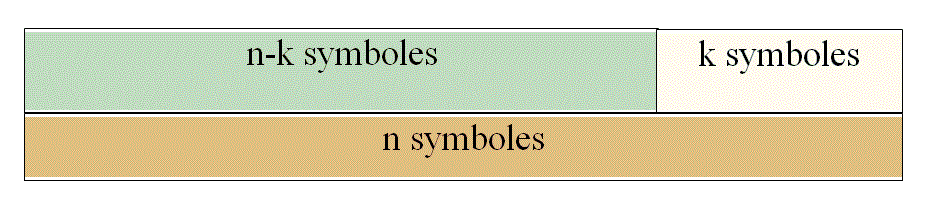
Le CRC est une méthode de codage qui consiste à grouper à l'émission les bits à transmettre en mots de "n-k" bits et à les associer à un mot de "n" bits. La redondance est constitué par les "k" bits. Le nombre de mots possibles de "n" éléments est de "2n-k" et les autres mots correspondent à des mots entachés d'erreurs.
Les méthodes de « vérification de clé » consistent à comprimer l'information. A partir d'une séquence d'information de longueur "n-k" finie, un mécanisme de compression (CRC - Cyclic Redundancy Check), caractérise cette séquence d'information à l'aide d'une information condensée : la clé. Cette clé ne permet pas de corriger les erreurs, elle permet de détecter les différences entre plusieurs séquences.
 |
1.1.Mécanisme de détection d'erreurs
Soient les données suivantes :
- mi = nombre de séquences d’information possédant la même clé.
- n-k = taille de la séquence d’information (fixe ou variable).
- k = taille de la clé (résultant de la division polynomiale).
- n = taille du message transmis.
Le mécanisme de vérification de clé consiste à comprimer un message composé de "n-k" symboles en un nombre fini de bits (k).
Chaque clé, de valeur résultante « Si » est représentative d'un nombre « mi » de séquences d'informations de taille fixe ou variable. La clé « Si », un mot de « k » bits, peut prendre « 2k » valeurs différentes.
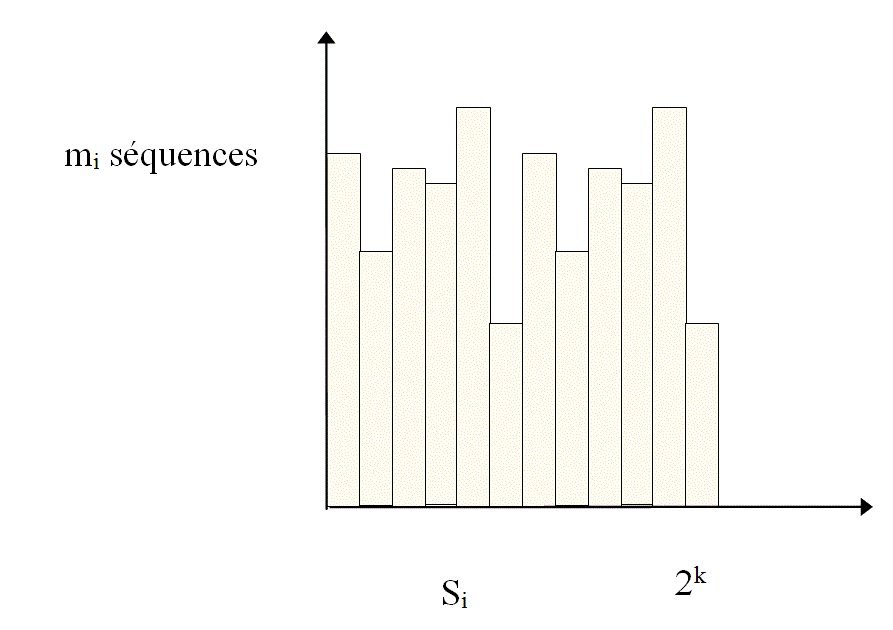 |
Pour une séquence d’information « mi » de taille « n » constant, il y a 2n formes possibles, et pour chacune de ces formes, il n'y a qu'une seule clé possible dont la valeur est comprise entre « 0 » et « 2k » et l'on obtient :
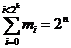
La probabilité de détection d'erreurs pour une séquence « mi » (représentée par sa clé « Si ») correspond à la probabilité d'obtenir la même valeur de clé « Si » à partir d'une séquence « mi » erronée.
La probabilité de détection d'erreurs associée à une clé « Si », 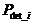 est définie de la façon suivante :
est définie de la façon suivante :
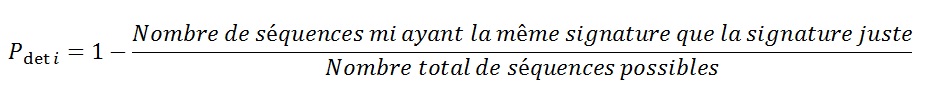
mi-1 : correspond au nombre de séquences mi ayant la même clé que la séquence exacte,
2n-1 : correspond au nombre total de séquences possibles (2n) moins la séquence juste (1).
Soit :
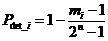
Afin de calculer le pouvoir de détection moyen, il faut sommer l’ensemble des cas correspondant aux "mi" séquences d’informations. Il existe mi séquences d'informations dont la probabilité de détection d'erreurs vaut Pdet_i. La valeur moyenne pour l'ensemble des « 2n » séquences possibles vaut :
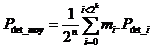
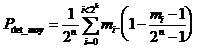
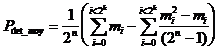
or
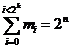 ,
,
d’ou
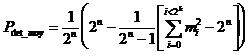
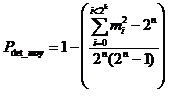
Dans le cas des réseaux de transmission, « n » n’est en général pas constant (les trames ont une longueur variable). De ce fait, les erreurs résiduelles sont composées de l’ensemble des combinaisons possibles d’erreurs sur les différentes longueur de trame.
Une séquence d'information « mi » peut donc s'écrire sous la forme suivante :
mi = « 2n-k + xi »,
nous obtenons donc :
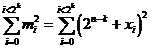
soit
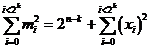
On déduit de la formule précédente que la probabilité de détection d'erreurs d'un mécanisme de compression est maximale lorsque mi est constant quel que soit Si,
on obtient mi = 2n-k :
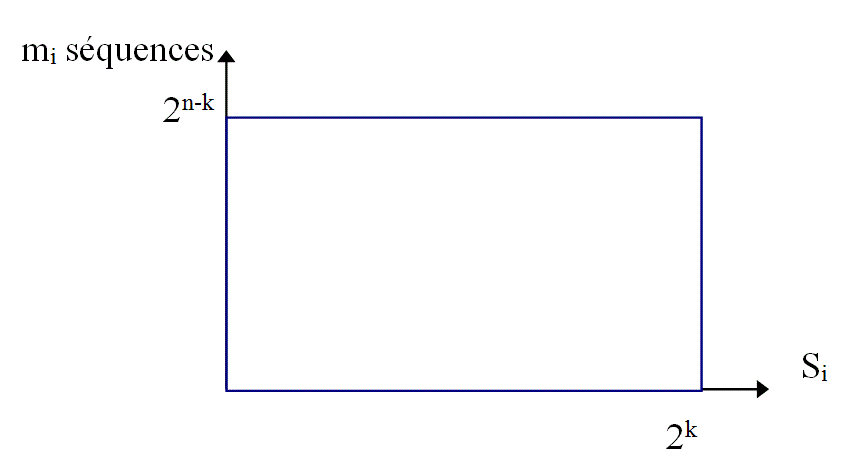
Et nous avons :
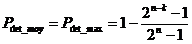
Lorsque la clé représente une nombre constant de séquences d’informations, le probabilité de détection d’erreur est optimale.
Dans le cas contraire, s’il existe un nombre différent de séquences d’informations, la probabilité de détection d’erreur sera inférieure à 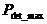 et devra être estimée au cas par cas.
et devra être estimée au cas par cas.
1.2.Propriétés et choix du polynôme générateur de clé
Les polynômes générateurs sont généralement classés selon les trois types suivants, quels que soit leur degré :
· les polynômes irréductibles,
- Un polynôme de degré k est irréductible s’il n’est pas divisible par un polynôme de degré inférieur à k, sauf par 1.
Par exemple,
a(x) = x4  x3
x3  x2
x2  x
x  1 de degré 4, et
1 de degré 4, et
b(x) = x8  x4
x4  x3
x3  x 1 de degré 8,
x 1 de degré 8,
sont des polynômes irréductibles.
les polynômes primitifs,
- Un polynôme irréductible de degré k est primitif si celui-ci est un diviseur du polynôme xn - 1, avec n = 2k - 1, sans être diviseur de tous les autres polynômes xm - 1 avec m < n. Il peut aussi être diviseur de certains polynômes xp - 1 avec p > n.
Les polynômes irréductibles ou primitifs sont obtenus par un algorithme mathématique complexe qu’il est fastidieux d’exécuter manuellement si le degré est élevé. A noter qu’il existe toujours des polynômes primitifs quels que soit le degré désiré.
· les polynômes quelconques (ni irréductibles et ni primitifs)
Un polynôme générateur de clé a pour objectif de détecter le maximum d'erreurs possibles. Pour cela il doit satisfaire aux règles suivantes :
1 - Soit la clé s(x) correspondant à la séquence d’entrée m(x) et obtenue en utilisant le polynôme générateur g(x) primitif et irréductible. Si nous appelons e(x) une séquence d’erreur, c’est-à-dire qui possède des « 1 » aux emplacements erronés et des « 0 » partout ailleurs, alors le message origine m(x) et le message erroné m(x)  e(x) ont la même clé s(x) si et seulement si e(x) est un multiple de g(x) modulo 2.
e(x) ont la même clé s(x) si et seulement si e(x) est un multiple de g(x) modulo 2.
Donc, la plus petite séquence erronée est g(x), d’où :
2 - Si le polynôme générateur est de degré k, toutes les erreurs pouvant affecter une séquence d’entrées de longueur n £ k sont détectées. Il est alors possible de déterminer le nombre de séquences erronées non détectées pour n ³ k, car elles sont toutes multiples de g(x).
Les séquences d’entrée de longueur n correspondent à des polynômes de degré n-1. Il y a donc 2n-1 séquences possibles car chaque polynôme a « n » coefficients et ceux-ci peuvent prendre les valeurs « 0 » ou « 1 ».
On démontre par récurrence qu’il y a N = 2n-k - 1 séquences erronées qui sont indétectables. Ainsi, pour m = n, on obtient 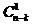 séquences erronées de base,
séquences erronées de base, 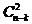 séquences erronées en combinant les séquences de base deux à deux, etc..., et enfin une séquence erronée en combinant toutes les séquences de base, soit
séquences erronées en combinant les séquences de base deux à deux, etc..., et enfin une séquence erronée en combinant toutes les séquences de base, soit 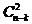 . D’où :
. D’où :
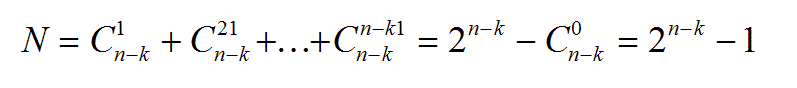
3 - Pour une séquence d’entrées de longueur « n » avec « n-k », la probabilité pour que le générateur de clé de degré k ne détecte pas d’erreurs, est égale à [2n-k-1]/[2n-1]. Ceci en supposant que toutes les séquences erronées ont une probabilité d’apparition identique. Lorsque n est très grand, le rapport tend vers 2-k. Cette propriété est la plus importante car elle caractérise avec précision le pouvoir de détection P de l’analyse de clé qui est presque uniquement fonction du degré du polynôme générateur choisi.
4 - Tout générateur de clé construit à partir d’un polynôme générateur qui possède au moins deux coefficients non nuls, détecte toutes les erreurs simples.
5 - Tout générateur de clé construit à partir d’un polynôme générateur contenant (xhÅ1) en facteur, détecte toutes les erreurs impaires.
6 - Tout générateur de clé construit à partir d’un polynôme générateur primitif de degré k, détecte toutes les erreurs simples et doubles si la séquence d’entrée est de longueur au plus égale à 2k - 1.
7 - Tout générateur de clé construit à partir d’un polynôme générateur de la forme g(x)=(x Å 1).f(x) avec f(x) polynôme primitif de degré k, détecte toutes les erreurs impaires et doubles, donc en particulier les erreurs simples, doubles et triples, si la séquence d’entrée est de longueur au plus égale 2k - 1.
8 - Tout générateur de clé construit à partir d’un polynôme générateur de degré k, détecte tous les types d’erreurs de longueur inférieure ou égale à k dans un message de longueur n (n > k).
9 - Si le polynôme générateur choisi est irréductible de degré k, alors il détecte ces erreurs répétitives avec une probabilité proche de 1-2-k. S’il n’est pas irréductible, il ne détecte ce type d’erreurs qu’avec une probabilité de 1-2-k/b, où b est la plus forte puissance relative au polynôme décomposé en facteurs irréductibles.
Ces propriétés montrent que le polynôme générateur joue un rôle capital, selon son type (primitif, irréductible, quelconque) et selon son degré. Même avec un polynôme de degré réduit, on constate que la vérification de clé est dotée d’un pouvoir de détection de fautes élevé, quelles que soient les hypothèses de fautes supposées.
A chaque code détecteur d'erreur est associé une distance caractéristique "la distance minimale de HAMMING".
Un code de distance dmin détectera toute les configurations de dmin - 1 erreurs.
1.3.Réalisation d’un C.R.C.
Deux méthodes permettent de réaliser le C.R.C :
· La division polynomiale
· La méthode du OU-Exclusif
1.3.1.La division polynomiale
Une suite d’informations numériques représente un message. A tout message est associé une représentation algébrique, c’est-à-dire un polynôme de degré n-1 si le message comprend n informations.
Le message m = [ an-1 a n-2 an-3 ... a 2 a1 a0 ] est associé à un polynôme m(x) :
m(x) = an-1.Xn-1  an-2.Xn-2
an-2.Xn-2  ...
...  a1.X1
a1.X1  a0 ,
a0 ,
où X est une variable muette et les coefficients ai des valeurs binaires. Par convention, le coefficient an-1 est le premier bit transmis et correspond au plus fort degré du polynôme. Par exemple, le message n=(1,0,1,1,0,0,0,1) donne le polynôme n(x) = x7  x5
x5  x4
x4  1.
1.
L’opérateur  (OU Exclusif) est utilisé car nous ne considérons que des valeurs binaires, chaque bit du message étant traité séparément. L’algèbre sur les polynômes modulo 2 se définit par les opérations binaires suivantes : l’addition, la soustraction, la multiplication et la division. En arithmétique modulo 2, l’addition et la soustraction sont identiques.
(OU Exclusif) est utilisé car nous ne considérons que des valeurs binaires, chaque bit du message étant traité séparément. L’algèbre sur les polynômes modulo 2 se définit par les opérations binaires suivantes : l’addition, la soustraction, la multiplication et la division. En arithmétique modulo 2, l’addition et la soustraction sont identiques.
La division polynomiale est une division de m(x) par g(x) qui consiste à chercher un quotient q(x) et un reste r(x) de degré inférieur à celui de g(x) tel que :
m(x) = [q(x)  g(x)]
g(x)]  r(x)
r(x)
ou : m(x) - [q(x)  g(x)] = r(x)
g(x)] = r(x)
Cette deuxième forme fait apparaître un mécanisme de soustractions successives où g(x) est décalé de k rangs à gauche, c’est-à-dire multiplié par xk, afin d’atteindre le monôme de plus haut degré de m(x). Alors, q(x) possède un monôme en xk.
Une séquence d’informations correspondant au polynôme m(x) est comprimée au moyen d’une division de m(x) par un polynôme générateur g(x). La clé est le résultat de cette division : soit le quotient, soit le reste selon le type de réalisation effectué.
Posons le polynôme générateur g(x) = xk + bn-1.xn-1 + ... + b1.x1 + 1
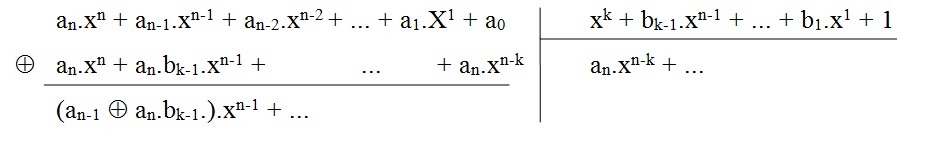
1.1.Réalisation pratique d’un C.R.C. par la méthode de la division polynomiale
Le principe de la division de deux polynômes peut être mis en oeuvre de façon :
- · matériel,
- · logiciel.
D’un point de vue matériel, des registres à décalage et des OU-exclusifs sont utilisés, et peuvent avoir une structure série ou parallèle. La clé est alors le reste de la division de m(x) par g(x) qui est le contenu final du registre à décalage
Pour la structure série, les données arrivent en série sur la ligne d’informations. Avec une structure parallèle, les données arrivent sur plusieurs lignes d’informations.
Les générateurs de clé série (voir Figure) et parallèle (voir Figure) construits à partir d’un même polynôme générateur primitif ont la même efficacité.
Dans la structure série présentée ci-dessous, les informations arrivent par l’entrée E, puis entrent dans le registre à décalage.
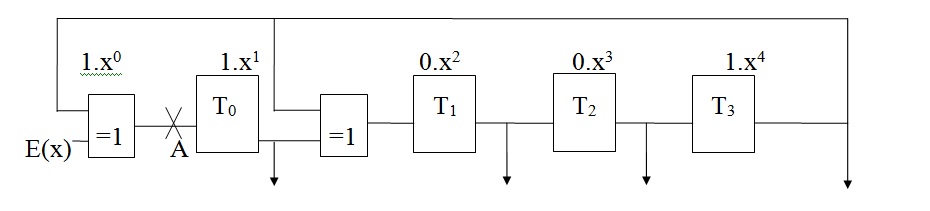
Figure : Générateur de clé de type SERIE avec g(x) = x4 + x + 1
Soit la séquence d’entrée (1,1,0,1,0,0,0,1,1), soit le polynôme d’entrée E(x) = x8+x7+x5+x+1.
Les états des registres sont décrits pour chaque front d’horloge dans le Tableau : Etats des registres d'un générateur de clé de type série.
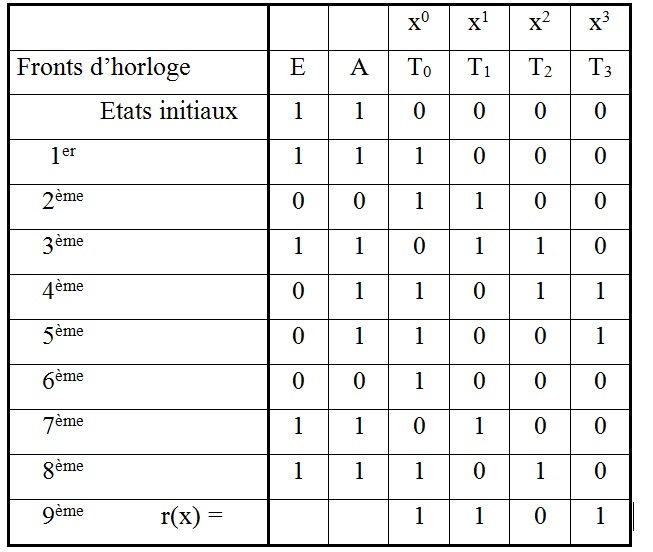
Tableau : Etats des registres d'un générateur de clé de type série
E(x) = [ q(x)  g(x) ]
g(x) ]  r(x)
r(x)
d’où E(x)/g(x) = q(x)  [ r(x)/g(x) ]
[ r(x)/g(x) ]
Le contenu final du registre est égal au reste de la division. De la même manière, nous pouvons construire un générateur à entrées parallèles.
Les informations en série notées (an-1, an-2, an-3, an-4, ..., a1, a0) sont groupées par bloc de 4, soient (an-1, an-2, an-3, an-4 / an-5, an-6, an-7, an-8 / ...) et présentées en parallèle sur chacune des entrées E0, E1,.E2, E3. En un seul front d’horloge, le résultat est établi pour ces 4 valeurs.
Soient y0, y1,.y2, y3, les états des registres à un instant « t » quelconque et a, b, c, d, les valeurs des registres évoluant suivant le Tableau : Etats des registres d'un générateur de type parallèle.
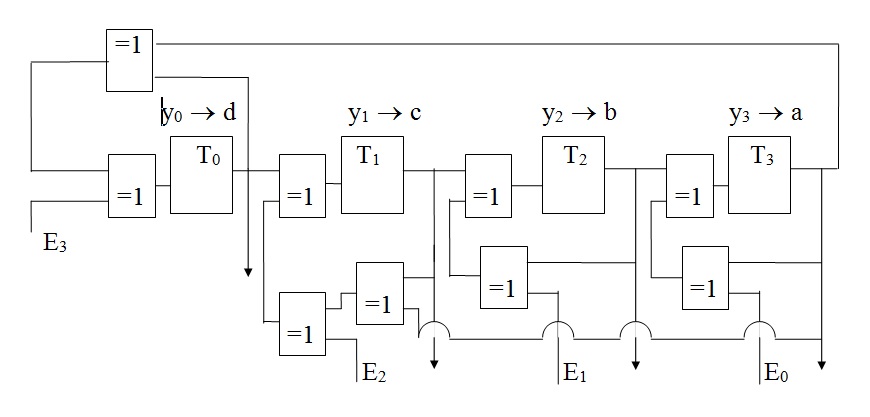
Figure : Générateur de clé à entrées parallèles avec g(x) = x4 + x + 1
La division polynomiale nécessite plus de cycles machine puisqu’il faut autant d’opérations (décalage + OU exclusif) que de bits contenus dans le message à contrôler.
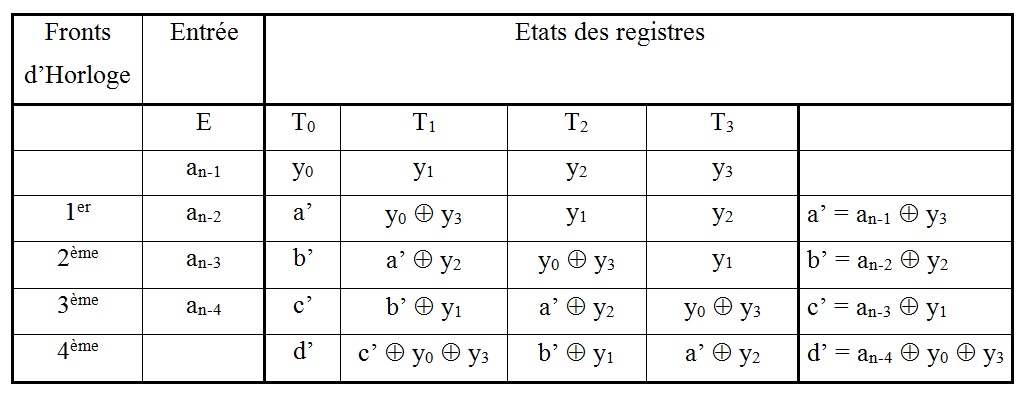
Tableau : Etats des registres d'un générateur de type parallèle
Nous obtenons les 4 fonctions suivantes :
a = a’  y2 = an-1
y2 = an-1  y3
y3  y2
y2
b = b’  y1 = an-2
y1 = an-2  y2
y2  y1
y1
c = c’  y0 = an-3
y0 = an-3  y3
y3  y1
y1  y0
y0
d = d’ = an-4  y0
y0  y3
y3
1.3.2.Méthode et réalisation pratique d’un CRC à partir d’un OU-Exclusif
Il existe une autre méthode afin de déterminer la clé. L’obtention d’une clé peut faire appel à un registre à décalage où certains bits sont bouclés sur l’entrée par l’intermédiaire de la fonction logique OU-Exclusif (Figure : Registre à décalage 16 bits (générateur de clé)). La clé correspond alors au contenu final du registre après passage en série de l’ensemble des informations. La longueur du registre ainsi que les bouclages sont fonction du polynôme P(x) qui, pour des applications usuelles, est généralement de degré 8 ou 16.
Soit P(x) = x16 + a15.x15 + a14.x14 + ... + a1.x + a0 avec a15 ... a0 = « 0 » ou « 1 »,
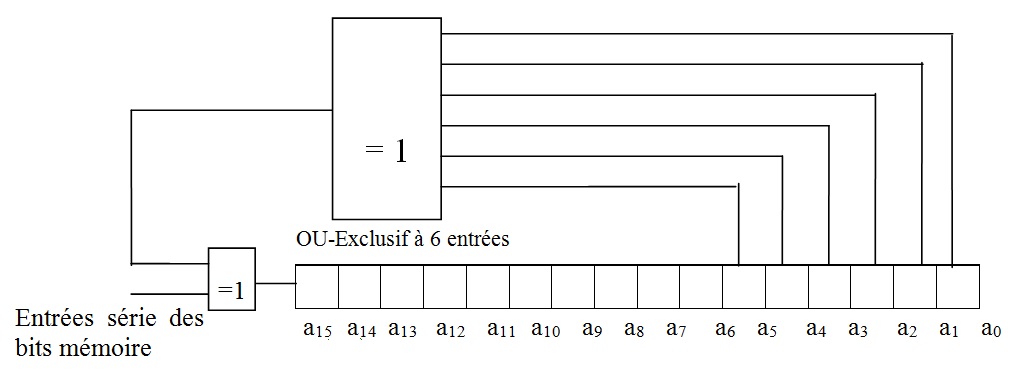
Figure : Registre à décalage 16 bits (générateur de clé)
La clé obtenue grâce à ce principe peut également être calculée par logiciel avec un algorithme adapté. L’algorithme correspondant s’obtient en observant le contenu du registre après 16 décalages successifs.
Si (y0 ... y15) est l’état initial du registre à t = 0 et (a0 ... a15) les 16 bits du message d’entrée, alors le contenu final du registre (x0 ... x15) après 16 décalages sera :
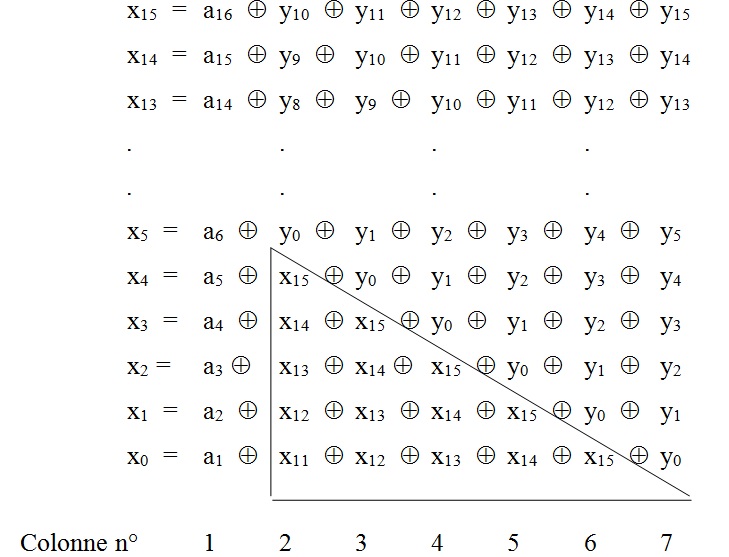
La colonne 1 représente la totalité du message d’entrée, les colonnes 2 à 7, hors la zone encadrée, représentent le contenu initial du registre décalé respectivement de 5 à 0 rangs.
Il ne reste plus alors qu’à effectuer les OU-Exclusifs entre les valeurs issues du bouclage (partie encadrée). Celles-ci seront déterminées par simple lecture à l’adresse pointée par l’adresse du début du tableau indexée de la valeur du quintuplet.
Ces valeurs seront lues directement dans un tableau de 25 = 32 éléments dans lequel on trouve, pour chaque quintuplet (x15, x14, x13, x12, x11), la valeur correspondante de x15, x15  x14, x15
x14, x15  x14
x14  x13 , x15
x13 , x15  x14
x14  x13
x13  x12, x15
x12, x15  x14
x14  x13
x13  x12
x12  x11.
x11.
1.4. Les codes correcteurs d’erreurs (codes de HAMMING).
Il est important de ne pas confondre distance de Hamming et codes de Hamming. Les codes de Hamming sont des codes détecteurs et correcteurs d’erreurs particuliers.
1.4.1.Principe des codes de Hamming
Si un transfert d’informations n’est pas correct, il existe 2 manières de retrouver la donnée :
· en demandant la ré-émission du message,
· en corrigeant l’erreur.
Il n’est pas toujours possible de demander une ré-émission du message. Le fait de corriger ces erreurs de transmission est alors primordial.
Les codes de Hamming permettent de détecter et de corriger les erreurs simples.
La méthode consiste à ajouter à un message de M digits, K digits de contrôle constituant ainsi un ensemble de (M + K) digits.
Il faut pour un mot de taille M digits, K digits de contrôle, or K digits ne permettent de définir que 2K combinaisons, d’où :
M + K + 1 £ 2K
Ce qui donne pour différente valeur de M, le tableau suivant :
|
M (bits) |
K (contrôle) |
|
4 |
3 |
|
8 |
4 |
|
16 |
5 |
|
32 |
6 |
1.4.2.Utilisation des Codes de Hamming
Pour montrer de quelle façon sont élaborés ces digits, on se place dans le cas d’un message de 4 digits (M = 4) ; 3 digits de contrôle (K = 3) sont alors nécessaires.
L’ensemble du message codé constitue alors un mot de 7 digits écrit sous la forme :
X = [ a1, a2, a3, a4, a5, a6, a7 ]
Les K digits de contrôle sont placés en a1, a2 et a4 sous réserve qu’il y en ait au moins un dans chacun des groupes (a1, a3, a5, a7), (a2, a3, a6, a7) et (a4, a5, a6, a7). Les digits de contrôle sont disposés de façon à ne contrôler que des digits « informatifs » et non d’autres digits de contrôle.
Les états des digits de contrôle sont donnés par les relations suivantes :
a1 = a3  a5
a5  a7
a7
a2 = a3  a6
a6  a7
a7
a4 = a5  a6
a6  a7
a7
Les codes de Hamming sont des codes détecteurs d’erreurs mais aussi correcteur d’erreurs. Il est donc possible de déterminer la position de l’erreur dans un message codé.
Dans notre exemple, l’erreur peut se placer parmi 7 positions. Il est alors nécessaire d’utiliser 3 bits pour coder en binaire la position de l’erreur dans le message codé.
La position de l’erreur se note en binaire [e3, e2, e1 ], et les états e3, e2 et e1 sont définis de la manière suivante : e1 = a1  a3
a3  a5
a5  a7
a7
e2 = a2  a3
a3  a6
a6  a7
a7
e3 = a4  a5
a5  a6
a6  a7
a7
A l’émission, les égalités e3 = e2 = e1 = 0 doivent être assurées, ce qui signifie qu’aucune erreur n’est détectée.
Si les égalités ne sont pas vérifiées, la position de l’erreur est indiquée dans le Tableau 3 : Position du bit erroné en fonction du code binaire de l’erreur ci-dessous :
|
Position de l’erreur |
e3 |
e2 |
e1 |
digit n° |
|
Aucune erreur |
0 |
0 |
0 |
|
|
a1 |
0 |
0 |
1 |
1 |
|
a2 |
0 |
1 |
0 |
2 |
|
a3 |
0 |
1 |
1 |
3 |
|
a4 |
1 |
0 |
0 |
4 |
|
a5 |
1 |
0 |
1 |
5 |
|
a6 |
1 |
1 |
0 |
6 |
|
a7 |
1 |
1 |
1 |
7 |
Tableau : Position du bit erroné en fonction du code binaire de l’erreur
X = [ a1, a2, a3, a4, a5, a6, a7 ] E = [e3, e2, e1 ]
Les codes de Hamming ne détectent pas l’erreur double. Pour y parvenir, un digit de contrôle supplémentaire (bit de parité) portant sur l’ensemble du message X est ajouté. La longueur du nouveau message codé est alors (M+K+1) digits. Après transmission du message, ce dernier est contrôlé afin de vérifier sa validité.
Si la parité globale est inexacte : le test précédent est appliqué au mot de (M+K) digits :
- · Si une erreur simple, double ou triple est détectée, elle est corrigée.
- · Si aucune erreur n’est détectée le mot est exact, l’erreur porte sur le dernier digit de contrôle global.
Si la parité globale est exacte, il y a 0 ou 2 erreurs ; le test de Hamming est appliqué.
- · Si aucune erreur n’est détectée, il n’y a pas d’erreur.
- · Si une erreur est détectée, il y a 2 erreurs, le mot est faux et aucune correction n’est possible.
French
